[資料分析&機器學習] ：線性分類-邏輯斯回歸 (Logistic Regression) 介紹

10月 15, 2018

[資料分析&機器學習] ：線性分類-邏輯斯回歸 (Logistic Regression) 介紹

[資料分析&機器學習] ：線性分類-邏輯斯回歸 (Logistic Regression) 介紹

News from: YJ.

前面Perceptron 能夠讓我們成功達成二元分類，但我們只能知道預測結果是A還是B，沒辦法知道是A、是B的機率是多少。這種應用在我們生活中非常常見，比如說我們要根據今天的溫度、濕度、風向來預測明天的天氣，通常我們會需要知道明天是晴天的機率以及雨天的機率，來決定是否帶傘具出門。如果使用Logistic Regression就可以幫我們達成這樣的目標!

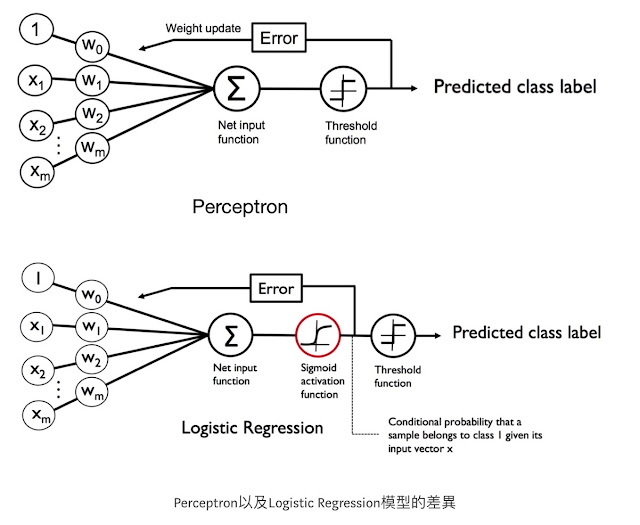
很重要的一點是Logistic Regression(邏輯斯回歸)很多人看名字以為是回歸的模型，但其實是一個分類的模型，名字取的不好很容易讓人誤解ＸＤ。這個分類的模型大致跟Perceptron類似，只是Perceptron是根據 w0*x0+w1*x1+…+wn*xn >0 或≤0來判斷成A或B類，而Logistic Regression則是一個平滑的曲線，當w0*x0+w1*x1+…+wn*xn越大時判斷成A類的機率越大，越小時判斷成A類的機率越小。由於是二元分類，如果判斷成A類的機率越小，B類的機率越大(判斷成B類的機率 = 1 - 判斷成A的機率)。

首現先介紹一下Sigmoid函數，也稱為logistic function，這個函數的y 的值介於 0~1，這樣的分布也符合機率是在0~1的範圍中。或許有人會覺得疑惑，Logistic Regression為什麼要用這個Logistic函數？其實也可以改用其他符合0~1的函數（因為機率的值是介於0~1），只是Logistic 函數是這種介於0~1的平滑函數中相對簡單的。

依下圖所示，當Z=0時判斷成+1類(A類)的機率為0.5，因此只要 z >0 判斷成 A類的機率就會>0.5 ，我們也就把它判斷成+1類(A類)。(這邊跟上一章perceptron一樣，只是多了機率的資訊) 如果z≤0 判斷成A類的機率就≤0.5 ，因此我們就把他判斷成-1類(B類)

接下來要說明要這個 Logistic Regression要怎麼找到一條線，將兩群做線性分類，最終的結果如下圖所示

Logistic Regression不需要像上一個Perceptron演算法需要去看一個一個的資料點來做更新，Logistic Regression有一個數學解的方法可以直接找到一組W！

為了數學推導方便，之前我們將二元分類的A類以+1表示、B類以-1表示，現在將A類改以+1表示、B類以0表示。我們想要找到一組w，能夠將下方的式子變成最大值，那組w就是我們要找的線(z=w*x)。下方的式子是希望當y=1的時候 ∅(z) 越靠近1（判斷成A類的機率越大），由於1-y是0所以右邊的項會是1，當y=0時左邊這項會是1右邊這項希望 ∅(z) 越靠近0越好（判斷成B類的機率越大）。